|
DOI: 10.25136/2409-7543.2018.3.26263
Дата направления статьи в редакцию:
11-05-2018
Дата публикации:
04-07-2018
Аннотация:
Недостаточные темпы экономического роста, проблемы в сфере безопасности, ожидаемый выход Великобритании из Евросоюза побуждают к дальнейшим исследованиям в сфере анализа процессов интеграции и дезинтеграции над- и межгосударственных образований. В работе представлена модель безопасности государства, состоящая из двух компонент – функции развития и функции сохранения. Функция развития в форме трехфакторной степенной производственной функции учитывает численность населения страны, площадь ее территории, урбанизацию, валовой внутренний продукт на душу населения и естественный прирост населения. Функция сохранения оперирует такими переменными, как: доля государствообразующего этноса от численности населения страны, параметры притяжения и этнической разнородности. Выполнена верификация модели безопасности на примере стран Евросоюза. Разработана модель безопасности над- и межгосударственных политических образований (союзов), учитывающая степень интеграции между отдельными странами (долю государственных функций, переданных в ведение союза). Для стран Евросоюза выполнена оценка параметра разнородности относительно союзообразующей страны – Германии. Рассмотрена модель сетевой структуры, включающая географический граф (совокупность вершин – государств, и ребер – наличие границ между ними) и социально-политический граф (дуги интерпретируются как наличие социально-политической связи). Дано определение допустимых коалиций. Сформулировано правило формирования социально-политических сетевых структур: политические акторы выбирают такую коалицию, при которой значение функции безопасности максимально. Приведены примеры формирования оптимальных коалиций. С использованием модели сетевой структуры выполнен анализ процессов интеграции и дезинтеграции в Евросоюзе. По мере развития интеграции Евросоюза ожидается усиление дезинтеграционных процессов в многонациональных государствах или выход их из Союза.
Ключевые слова:
модель безопасности, функция развития, функция сохранения, параметр этнической разнородности, социально-политический граф, коалиция, правило выбора, интеграция, дезинтеграция, национальная безопасность
Abstract: Insufficient economic growth rates, security problems, the expected exit of the UK from the EU prompt further research into the analysis of the processes of integration and disintegration of supra- and interstate entities. The paper presents a security model of the state, consisting of two components - development functions and conservation functions. The development function in the form of a three-factor power production function takes into account the population size of the country, its area, urbanization, gross domestic product per capita and natural population growth. The conservation function operates with variables such as: the share of the state-forming ethnos from the population of the country, the parameters of attraction and ethnic heterogeneity. The verification of the security model was carried out using the example of the EU countries. A model for the security of supra- and interstate political entities (unions) is developed, taking into account the degree of integration between individual countries (the share of state functions transferred to the Union). For the EU countries, an assessment of the heterogeneity parameter relative to the allied country, Germany, has been carried out. Shumov analyzes the network structure model that includes the geographic graph (combination of axes (states) and ridges (boundaries between states)) and sociopolitical graph (arcs are interpeted as the presence of sociopolitical connections). The author offers his definition of admissible coalitions and explains the rule of formation of socio-political network structures: political actors select coalition with the maximum security function. Shumov provides examples of formation of optimal coalitions. Using the network structure model, the author carries out an analysis of the processes of integration and disintegration in the European Union. As the European Union integration develops, disintegratoin processes are expected to reinforce in multinational states, or the states will have to leave the Union.
Keywords: security model, development function, conservation function, ethnic heterogeneity parameter, socio-political graph, coalition, selection rule, integration, disintegration, national security
1. Введение
Важнейшей научной и практической проблемой является организация «мониторинга геополитических процессов и их влияния на формирование угроз национальной безопасности Российской Федерации в пограничном пространстве» [5]. Для решения названной проблемы нужны как фактические данные, так и математические модели безопасности государств и надгосударственных образований.
Проблема поиска оптимальных размеров над- и межгосударственных образований исследуется, в частности, с помощью политико-экономических моделей [9], основанных на дихотомии производства общественных благ и их потребления. Чем больше государство, тем ниже удельные издержки производства общественных благ (включая, безопасность) и прочих услуг, которые это государство предоставляет гражданам. Поэтому крупные государства обладают преимуществом большого внутреннего рынка. Но если население большой страны слишком разнородно, то ее гражданам трудно прийти к согласию, какие именно общественные блага должно предоставлять государство, каким должен быть размер государства и, следовательно, уровень налогообложения. Тогда возникают тенденции к дезинтеграции страны.
Например, после вхождения некоторой страны в Европейский Союз (ЕС), темпы роста ВВП на душу ее населения, как правило, снижались относительно среднемировых (за исключением Великобритании, Бельгии, Ирландии, Польши и др.) [10]. Можно предположить, что созданные институты единого рынка, общего таможенного пространства, единая валюта, направленные на снижение удельных издержек, нейтрализуются другими неэкономическими механизмами и институтами. Многими исследователями отмечается, что Евросоюз страдает от глубокого кризиса идентичности, созданные институты плохо управляемы, избыточное регулирование душит конкуренцию, ЕС отдалился от избирателей и утратил живую связь с ними.
Недостаточные темпы экономического роста, проблемы в сфере безопасности (нелегальная миграция, терроризм), ожидаемый выход Великобритании из ЕС побуждают к дальнейшим исследованиям в сфере анализа процессов интеграции и дезинтеграции над- и межгосударственных образований с использованием различных подходов, включая математическое моделирование.
Для исследования социальных процессов математические методы стали применяться с начала – середины XX века: уравнения динамики боя Осипова–Ланчестера (1915–1916), теория игр в экономике (Дж. фон Нейман, О. Моргенштерн, 1944), математические методы в политологии и геополитике (Дж.Мангейм, Р. Рич, 1997; А.А. Акаев, С.Ю. Малков, 2009), модели исторических процессов и демографии (С.А. Нефедов, 2002), математические модели корпорации РЭНД в области национальной безопасности и др. В последнее десятилетие существующий разрыв в отечественной науке по использованию математических методов и компьютерного моделирования в сфере социально-политических наук стал преодолеваться. О чем свидетельствует множество публикаций в российских научных журналах, докладах на международных конференциях по кибернетике, теории активных систем, социофизике и социоинженерии. Внедрение в общественную практику и в государственную статистику информационных технологий и систем создают предпосылки для перехода от преимущественно качественных рассуждений в области национальной безопасности и геополитики к сочетанию качественных методов и количественных моделей.
Настоящая работа посвящена исследованию процессов интеграции и дезинтеграции над- и межгосударственных союзов математическими методами и ориентирована на специалистов в сфере национальной безопасности и геополитики.
2. Модель безопасности государства и союза государств
В Стратегии национальной безопасности России от 31.12.2015 г. под национальной безопасностью понимается состояние защищенности личности, общества и государства от внутренних и внешних угроз, при котором обеспечиваются реализация конституционных прав и свобод граждан, достойные качество и уровень их жизни, суверенитет, независимость, государственная и территориальная целостность, устойчивое социально-экономическое развитие страны.
Предметом нашего исследования являются социальные группы, общности, народы, государства, т.е. ценности, которые по своей природе дуалистичны (двойственны): добро и зло, свобода и ответственность, развитие и сохранение, конкуренция и кооперация. Иными словами, безопасность есть процесс и результат деятельности человека и социальных (государственных) институтов на основе разрешения дихотомии ценностей развития (суверенности) и сохранения. Нас будет интересовать главным образом онтологическая безопасность (ontological security), означающая присущее людям чувство безопасности, упорядоченности и правильности их жизни. Наиболее отчетливо это чувство ощущается в случае устойчивой личной идентичности, не изменяющейся с течением времени [1]. Например, если в случае военного поражения страны она частично утрачивает политический суверенитет, но остальные сферы жизни неизменны (этнический состав, культура, язык и т.д.), то данная страна обладает онтологической безопасностью (самовоспроизводимостью). Если же в случае длительных миграционных процессов существенно меняется этнический состав населения (Западная Римская империя в IV – V веках), то, несмотря на политический суверенитет, ее онтологическая безопасность уже разрушена, поскольку носитель романского языка и культуры фактически растворился среди других народов.
В логике высказываний дихотомии пары ценностей (их непреодолимой связности) можно поставить в соответствие бинарную связку конъюнкции & («и», логическое умножение). В математике дихотомии соответствует мультипликативная функция. Следовательно, безопасности i-го государства можно поставить в соответствие функцию ui безопасности [8]:
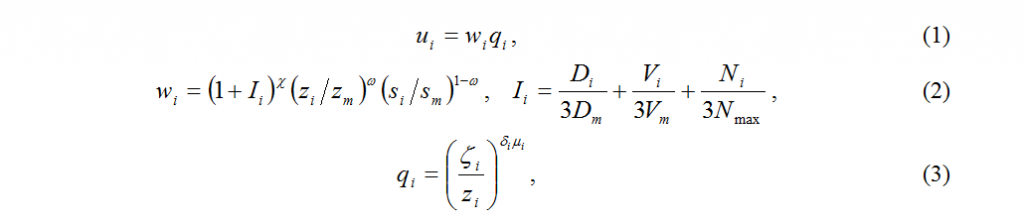
где: wi – функция развития (суверенности) i-го государства;
qi – функция его сохранения;
Ii – индекс социальных технологий i-й страны;
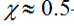 –степень социально-технологического фактора; –степень социально-технологического фактора;
zi – численность населения i-й страны;
si – ее площадь;
sm – площадь крупнейшей страны (России);
zm – численность населения самой многочисленной страны (Китая);
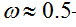 – параметр эластичности по демографическому фактору; – параметр эластичности по демографическому фактору;
Di – доля городского населения в i-й стране;
Vi – ВВП на душу населения i-й страны;
Ni – прирост населения i-й страны;
Dm,Vm,Nm – максимальные значения указанных показателей;
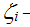 – численность государствообразующего этноса; – численность государствообразующего этноса;
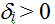 – параметр притяжения государствообразующего этноса i-й страны; – параметр притяжения государствообразующего этноса i-й страны;
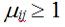 – параметр этнической разнородности. – параметр этнической разнородности.
Суверенитет, суверенное развитие является общественным благом, поэтому функция развития определена с использованием неоклассической производственной функции от ресурсов zi и si:
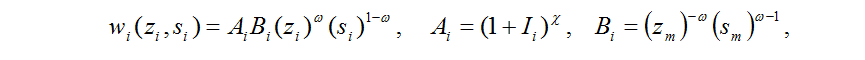
удовлетворяющей следующим условиям:
1) при отсутствии одного из ресурсов производство (суверенитет, развитие) невозможно:
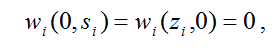
2) с ростом ресурсов суверенитет увеличивается:
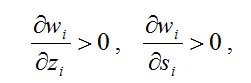
3) с увеличением ресурсов скорость роста суверенитета замедляется:
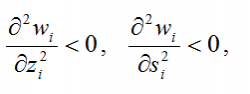
4) в связи с ограниченностью ресурсов значение функции суверенитета ограничено:
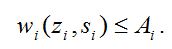
Из названных условий, в частности, следует: 0 < 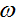 < 1. С точки зрения политологии [4] и военной теории и практики [2] основной задачей вооруженных сил государства является защита суверенитета и территориальной целостности страны. Исходя из положения: численности вооруженных сил государств отражают их базовый суверенитет, - методом наименьших квадратов вычислена оценка параметра эластичности: < 1. С точки зрения политологии [4] и военной теории и практики [2] основной задачей вооруженных сил государства является защита суверенитета и территориальной целостности страны. Исходя из положения: численности вооруженных сил государств отражают их базовый суверенитет, - методом наименьших квадратов вычислена оценка параметра эластичности:
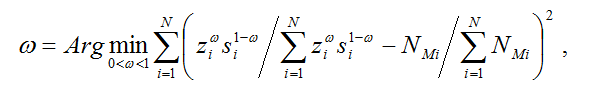
где: N – количество государств; NMi – численность вооруженных сил i-го государства. Используя численности вооруженных сил крупнейших государств мира по состоянию на 2006 г. для N = 87 получено 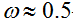 . .
Коэффициент корреляции между значениями индекса Ii социальных технологий и значениями глобального индекса инноваций (GII) для сорока крупнейших по численности населения государств равен 0,75. То есть, с достаточной для многих практических задач точностью вместо индекса GII (учитывающего около 80-ти показателей, многие из которых оцениваются экспертами), можно использовать индекс Ii, учитывающий всего три показателя: урбанизацию (прошлое, достигнутый уровень иерархии в ходе исторического развития), ВВП на душу населения (настоящее) и темпы естественного прироста населения (будущее).
Известно, что крепость социальных институтов любого государства поверяется войной. Участие регионов (союзников, доминионов) в войне оценивается потерями (убитыми и раненными). Причем наибольшие потери несет союзообразующая страна (регион). «Эффективная» (с точки зрения участия в победе) численность населения союза равна:
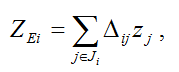
где: Ji – множество стран, являющихся союзниками (доминионами) i-й страны, включая союзообразующее государство (метрополию); 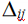 – отношение доли погибших в j-й стране к доли погибшим в метрополии (i-й стране). – отношение доли погибших в j-й стране к доли погибшим в метрополии (i-й стране).
Следовательно, социальные технологии союзного центра (метрополии) обеспечили увеличение его базового суверенитета за счет привлечения союзников (доминионов), т.е.
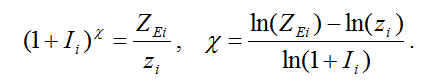
По опыту участия Великобритании. Франции и их колоний в первой мировой войне получено 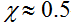 . В частности, население французской метрополии в годы войны потеряло убитыми и раненными около 3 % численности населения, тогда как население французских колоний – около 0,4 % численности населения, т.е. примерно в 7 раз меньше. . В частности, население французской метрополии в годы войны потеряло убитыми и раненными около 3 % численности населения, тогда как население французских колоний – около 0,4 % численности населения, т.е. примерно в 7 раз меньше.
Таким образом, факт многолетнего владения некоторыми территориями и населением (колониальные владения, находящиеся под властью метрополии) обеспечивает определенное участие подвластного населения в решении жизненно важных задач метрополии, причем с риском для жизни. Соучастие властей и граждан колоний в делах метрополии увеличивает суверенитет метрополии и количественно характеризуется нижней оценкой степени технологического фактора 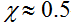 . .
Верхняя оценка степени технологического фактора находится для отдельных сфер деятельности. В частности, применительно к экономике для оценки роли крупнейшей экономической державы можно использовать значение 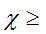 1,2–1,4. Содержательно верхняя оценка степени характеризует возможности государств по формированию наднациональных институтов, привлечению союзников, расширению зоны национальных интересов [8]. 1,2–1,4. Содержательно верхняя оценка степени характеризует возможности государств по формированию наднациональных институтов, привлечению союзников, расширению зоны национальных интересов [8].
Известен постулат Н. Тельновой: познаваемость сложных иерархических социальных систем как следствие принципа самоподобия. Принцип самоподобия означает возможность суждения о целом по его части. По отдельным поступкам можно судить о субъекте, по субъектам – об обществе, по обществу – об общем состоянии мира [7].
Для определения функции сохранения использовано распределение Парето, обладающее свойством самоподобия. Использование свойства самоподобия и распределения Парето позволит с единых позиций описывать сложные иерархические системы безопасности, где на нижних уровнях различия обусловлены возрастными, психологическими и иными характеристиками людей. На средних уровнях часть различий игнорируется и рассматриваются преимущественно социально-экономические и этнические характеристики, а на высших уровнях – цивилизационные характеристики.
Функция сохранения имеет два параметра: этнической разнородности и притяжения. Для оценки параметра разнородности между этносами i и j используется выражение:
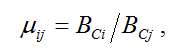
где: BCi – доля потерь в войне от численности государствообразующего этноса i; BCj – доля потерь от численности этноса j. Второй способ оценки параметра разнородности (вычисление межэтнических расстояний) основан на анализе межэтнических браков по данным переписи населения России 2010 г. [6]. В таблице 1 показаны значения межэтнических расстояний Dij и параметра разнородности (по результатам участия национальностей в Великой Отечественной войне) относительно русского этноса.
Таблица 1. Межэтнические расстояния и параметр разнородности
|
№
|
Национальность
|
Расстояние Dij
|
Параметр разнородности 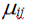
|
|
1
|
Украинцы
|
0,66
|
1,2
|
|
2
|
Мордва
|
0,68
|
1,3
|
|
3
|
Удмурты
|
0,71
|
1,5
|
|
4
|
Армяне
|
0,74
|
1,5
|
|
5
|
Чуваши
|
0,75
|
1,3
|
|
6
|
Татары
|
0,84
|
1,3
|
|
7
|
Казахи
|
0,97
|
1,4
|
|
8
|
Азербайджанцы
|
1,03
|
2,3
|
|
9
|
Башкиры
|
1,55
|
1,5
|
|
10
|
Чеченцы
|
2,03
|
12,6
|
Коэффициент корреляции между значениями межэтнических расстояний и параметра разнородности (после их масштабирования и сдвига) равен 0.93.
Поскольку безопасность государств оценивается не только исследователями, но и тысячами граждан, мигрирующих из одних стран в другие в поисках лучших условий жизни и безопасного существования, то для оценки параметра di притяжения использовались данные по миграции населения и уровню социально-экономического развития регионов страны. В частности, получены следующие значения параметра [8]:
|
Россия
|
США
|
Германия
|
Казахстан
|
Украина
|
|
0,1–0,5
|
0,3–0,8
|
0,2–2,4
|
0,8–1,3
|
0,8–1,4
|
Меньшим значениям параметра притяжения соответствуют лучшие возможности этноса по созданию устойчивых государственных образований. Отметим, что в мире существует множество народов, не создавших свое государство (курды, баски, каталонцы, цыгане и др.), т.е. имеющие большие значения параметра притяжения.
Имея модель безопасности с простыми и измеримыми параметрами, для любого государства можно выполнить расчеты за достаточно большой исторический период. На рис. 1 показаны значения функции безопасности 4-х крупнейших государств мира.
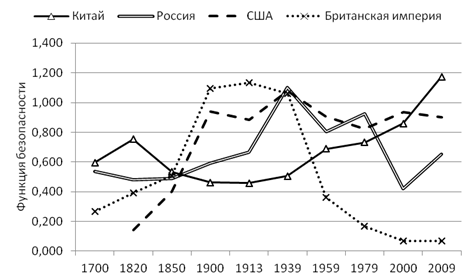
Рис. 1. Значения функции безопасности крупнейших государств мира
В результате высоких темпов естественного роста численности населения и в силу других причин Англия стала крупнейшей морской державой, мастерской мира, заселила своими колонистами многие земли в разных частях света. Столетие (1815–1914 гг.) Великобритания конкурировала с Российской империей в борьбе за наследство Османской империи, Персии и Цинского Китая. Расцвет могущества Британской империи одновременно сопровождался уменьшением доли «белого» населения, высокими затратами на поддержание имперских институтов, и, как следствие, снижением эффективности империи. Период с 1945 г. по 1991 г. прошел под знаком конкуренции двух сверхдержав – США и СССР. Настоящее время характеризуется уходом от однополярного мира и увеличением экономического и политического влияния КНР.
На рис. 2 показаны значения функции безопасности и ее компонент для России.
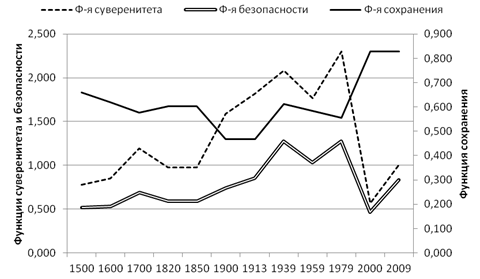
Рис. 2. Значения функции безопасности и ее компонент России
Из рисунка видно, что революциям (модернизациям) 1917 г. и 1991 г. предшествовали периоды спада значений функции сохранения. Основным результатом революции 1917 года стало увеличение доли государствообразующего этноса с 43% до 58%, а результатом модернизации 1991 года – увеличение его доли с 52% до 81%.
Безопасность государств оценивается и обычными гражданами, мигрирующими из одних стран (регионов) в другие в поисках лучших условий жизни и безопасного существования.
На рис. 3 показаны значения функции развития России (функция сохранения считается константой, т.к. переписи населения с учетом изменений этнического состава проводятся раз в 10 лет) и сальдо межстрановой миграции, чел. Коэффициент корреляции между значениями функции развития и сальдо межстрановой миграции равен 0,86.
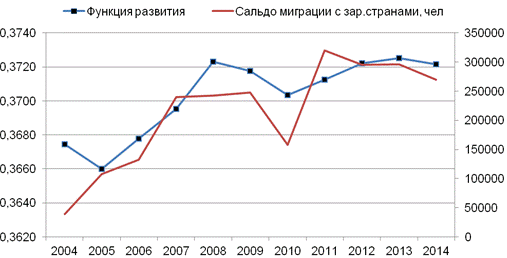
Рис. 3. Значения функции развития России и сальдо межстрановой миграции
На рис. 4 показаны значения функции безопасности стран Евросоюза и коэффициента миграции из внешних стран (Сирия, Индия, Марокко, Пакистан и др.) за 2010-2016 гг. Коэффициент корреляции между показателями равен 0,83.
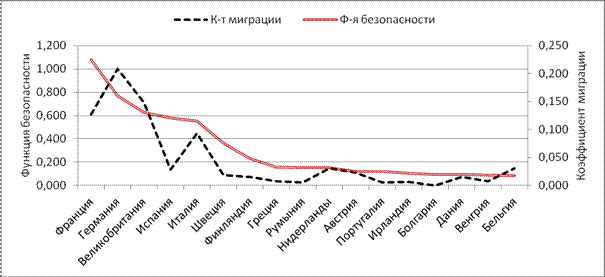
Рис. 4. Значения функции безопасности и коэффициента миграции стран Евросоюза
Имея модель безопасности и прогнозные значения, публикуемые органами государственной статистики и научными организациями по демографии и другим показателям, можно строить количественные прогнозы по следующим направлениям:
- мониторинг, анализ и прогнозирование роли и места государств в мировой и региональной политике;
- прогнозирование геополитической и региональной инверсии (смены глобальных и региональных государств – лидеров);
- прогнозирование мировой и региональной миграции населения и оценка ее влияния на безопасность государств и др.
Положим, что функция суверенитета Союза (меж- или надгосударственного образования) есть сумма значений функций суверенитета (возможно, взятая с определенным весовым коэффициентом), а функция сохранения подчиняется распределению Парето (в силу свойства самоподобия). Тогда безопасность Союза вычисляется по формулам:
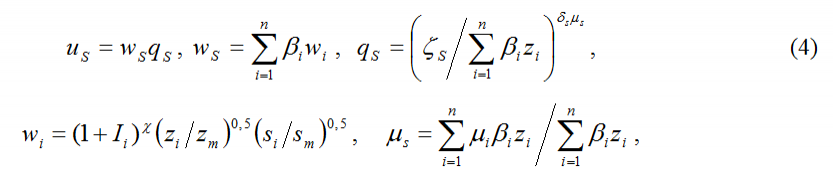
где: wS – функция суверенитета Союза; qS – функция сохранения; n – количество стран – членов Союза; 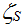 – численность населения союзообразующей страны (стран); zi – численность населения i-й страны; – численность населения союзообразующей страны (стран); zi – численность населения i-й страны; 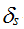 – параметр притяжения союзообразующей страны (стран); – параметр притяжения союзообразующей страны (стран); 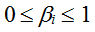 – степень участия i-й страны в Союзе (доля государственных функций, переданных в ведение Союза). – степень участия i-й страны в Союзе (доля государственных функций, переданных в ведение Союза).
Совокупность параметров 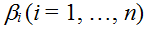 отражает вид государственного (межгосударственного) устройства Союза. При отражает вид государственного (межгосударственного) устройства Союза. При 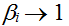 мы имеем унитарное государство. При понижении значений мы имеем унитарное государство. При понижении значений 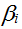 выполняется переход к федерации, конфедерации, содружеству и т.д. На примере Британской империи мы видим, что для разных стран значения параметра выполняется переход к федерации, конфедерации, содружеству и т.д. На примере Британской империи мы видим, что для разных стран значения параметра 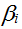 существенно отличались (коронные земли, протекторат, доминионы и т.д.). существенно отличались (коронные земли, протекторат, доминионы и т.д.).
Поскольку Евросоюз – это относительно новое политическое образование, не являющееся непосредственным наследником (по составу основных этносов или народов) существовавших на территории Западной Европы над- или межгосударственных образований, то параметр разнородности должен включать несколько частных показателей. Полагая, что союзообразующим государством является Германия (самое крупное по численности населения и объему ВВП государство – член ЕС), частными показателями разнородности государств могут быть:
· показатель 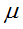 (1), характеризующий отношение к Германии в годы второй мировой войны; (1), характеризующий отношение к Германии в годы второй мировой войны;
· показатель 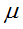 (2) суверенного исторического развития государства; (2) суверенного исторического развития государства;
· показатель 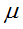 (3) географической разнородности. (3) географической разнородности.
Первый показатель позволит учесть отношение других народов и правительств к предыдущему интеграционному проекту Германии. Однако только его использование будет неполным, так как нынешний проект реализуется в иных исторических условиях, носит мирный характер и затрагивает интересы почти всех стран Европы, включая бывших противников Германии и нейтральные страны.
Учет второго показателя представляется важным, поскольку дальнейшая интеграция стран Евросоюза предполагает ограничение национальных суверенитетов. Как показывает исторический опыт, у разных стран ценность суверенности и самостоятельного развития различна.
В таблице 2 представлены результаты расчета параметров разнородности стран относительно Германии [8].
Таблица 2. Значения параметров разнородности стран – членов Евросоюза относительно союзообразующей страны (Германии)
|
№
|
Страна
|
Показатель
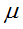 (1) (1)
|
Показатель
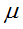 (2) (2)
|
Показатель
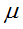 (3) (3)
|
Среднее геометрическое
|
Среднее арифметическое
|
|
1
|
Германия
|
|
|
|
|
|
|
2
|
Франция
|
4
|
6,9
|
3,8
|
4,72
|
4,90
|
|
3
|
Бельгия
|
4
|
2,1
|
3,4
|
3,04
|
3,16
|
|
4
|
Италия
|
2
|
3,0
|
5,6
|
3,21
|
3,51
|
|
5
|
Нидерланды
|
4
|
3,7
|
3,2
|
3,65
|
3,66
|
|
6
|
Великобритания
|
10
|
8,2
|
5,1
|
7,47
|
7,77
|
|
7
|
Дания
|
4
|
5,0
|
2,8
|
3,83
|
3,93
|
|
8
|
Ирландия
|
3
|
1,3
|
6,9
|
2,97
|
3,73
|
|
9
|
Греция
|
5
|
1,6
|
9,0
|
4,13
|
5,19
|
|
10
|
Испания
|
3
|
6,1
|
6,9
|
5,01
|
5,32
|
|
11
|
Португалия
|
3
|
5,6
|
8,9
|
5,31
|
5,84
|
|
12
|
Австрия
|
1
|
4,8
|
3,1
|
2,46
|
2,97
|
|
13
|
Финляндия
|
2
|
2,4
|
4,8
|
2,84
|
3,07
|
|
14
|
Швеция
|
3
|
4,0
|
4,8
|
3,87
|
3,94
|
|
15
|
Венгрия
|
2
|
1,7
|
4,6
|
2,51
|
2,77
|
|
16
|
Польша
|
4
|
2,2
|
3,1
|
3,04
|
3,12
|
|
17
|
Чехия и Словакия
|
2
|
1,6
|
3,5
|
2,23
|
2,36
|
|
18
|
Словения
|
8
|
1,1
|
4,7
|
3,41
|
4,58
|
|
19
|
Эстония
|
7
|
1,1
|
5,3
|
3,41
|
4,45
|
|
20
|
Латвия
|
7
|
1,1
|
4,9
|
3,35
|
4,33
|
|
21
|
Литва
|
7
|
1,1
|
4,8
|
3,34
|
4,31
|
|
22
|
Болгария
|
2
|
1,4
|
8,1
|
2,81
|
3,81
|
|
23
|
Румыния
|
2
|
1,7
|
6,9
|
2,88
|
3,54
|
По определению О. Коши средним значением является любое число, заключенное между наименьшим и наибольшим из значений множества. Поскольку среднее геометрическое не больше среднего арифметического (неравенство о средних), то оптимистической оценкой параметра разнородности будет среднее геометрическое. Выбор среднего геометрического можно обосновать и тем, что нами использовались относительные характеристики явлений различной природы.
Значение параметра притяжения для Германии равно: 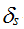 = 0,30 – 0,55. При значениях степени участия стран в Евросоюзе b1 = 1, bi = 0,5, i = 2, …, 23 (федерация) на рис. 5 показаны значения компонентов функции безопасности Евросоюза как надгосударственного объединения. = 0,30 – 0,55. При значениях степени участия стран в Евросоюзе b1 = 1, bi = 0,5, i = 2, …, 23 (федерация) на рис. 5 показаны значения компонентов функции безопасности Евросоюза как надгосударственного объединения.
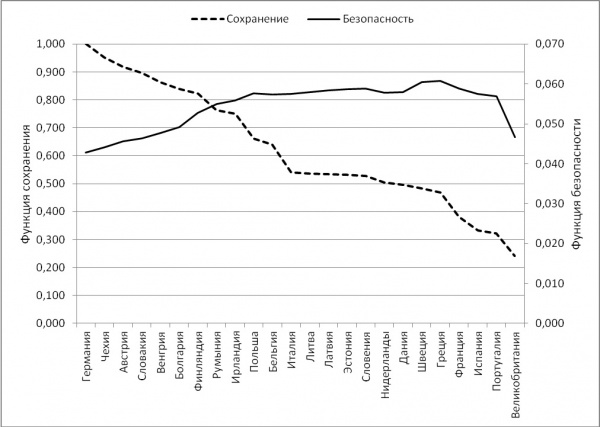
Рис. 5. Компоненты функции безопасности Евросоюза (bi = 0,5)
Из рисунка видно, что устойчивая федерация (значение функции сохранения не ниже 0,6) состоит из одиннадцати стран: Германия, Чехия, Австрия, Словакия, Венгрия, Болгария, Финляндия, Румыния, Ирландия, Польша и Бельгия. При этом значение функции безопасности равно 0,057.
Расчеты показывают, что в существующем ныне составе Европейский Союз является неустойчивым объединением и не сможет перейти к федеративному устройству. Рассмотренная модель безопасности расширяет и дополняет математические модели оценки геополитического потенциала государств и союзов государств и объясняет известный факт: несмотря на высокий совокупный потенциал стран ЕС (500 миллионов человек населения, 23% мирового ВВП), Евросоюз обладает крайне низкой политической субъектностью и обычно следует в фарватере политики США. Этот факт объясняется низким значением функции сохранения Евросоюза.
В этой связи представляется актуальной и важной задача поиска устойчивых в том или ином смысле государственных образований.
3. Модель сетевой структуры коалиций политических акторов
Пусть имеется множество N = {1, …, n} политических акторов (регионов, государств, административно-этнических единиц), занимающих некоторую ограниченную территорию. Выбор конкретного множества N зависит от прикладной задачи. Если рассматривается задачи устойчивости надгосударственного образования, то в качестве элементов множества N могут выступать существующие государства. Если речь идет об исследовании безопасности некоторого государства, то акторами будут его административно-этнические единицы.
Определение 1. Административно-территориальным (географическим) графом называется неориентированный граф 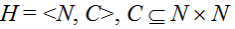 с матрицей смежности h = <N, C> (квадратной матрицей), элемент которой hij равен единице при наличии общей границы между акторами i и j, и нулю в противном случае. Положим по определению hii = 1, i = 1, …, n. с матрицей смежности h = <N, C> (квадратной матрицей), элемент которой hij равен единице при наличии общей границы между акторами i и j, и нулю в противном случае. Положим по определению hii = 1, i = 1, …, n.
Отдельной договоренности заслуживает вопрос об общей границе между государствами, разделенными морем. Например, о наличии общей границы Германии с Великобританией, Исландией или Канадой. Здесь может потребоваться доопределение с учетом расстояния между странами, разделенными морем.
На рис. 6 показан пример географического графа. Вершины графа нумеруются в порядке убывания значений функции безопасности, т.е. из i < j следует: ui > uj (в случае равенства значений функции безопасности меньший номер присваивается актору с большим значением численности государствообразующего этноса).

Рис. 6. Географический граф (вершины – политические акторы, ребра – наличие общей границы между ними)
Матрица смежностей h графа H симметрична и имеет вид:
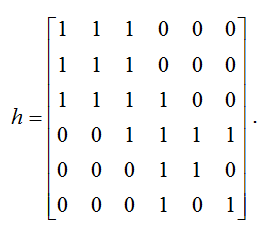
Положим, что с предложением на установление социально-политической связи ij со степенью интеграции 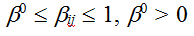 может обратиться актор с меньшим номером, т.е. i < j. Желание i-го актора образовать связь ij опишем переменной xoutij, которая равна единице, если актор хочет установить связь ij, и равна нулю в противном случае. Согласие актора j на установление связи ij опишем переменной xinji. Если xinji =1, то актор j принимает предложение актора i на установление связи, иначе xinji = 0. может обратиться актор с меньшим номером, т.е. i < j. Желание i-го актора образовать связь ij опишем переменной xoutij, которая равна единице, если актор хочет установить связь ij, и равна нулю в противном случае. Согласие актора j на установление связи ij опишем переменной xinji. Если xinji =1, то актор j принимает предложение актора i на установление связи, иначе xinji = 0.
Определение 2 [3]. Действием xi актора i в сетевой игре называется пара xi = (xouti, xini) векторов xouti = (xouti1,...,xoutin), xini = (xini1,...,xinin).
Иными словами, действие актора определяет множество его оппонентов, с которыми актор хочет установить исходящую связь, и множество оппонентов, на образование входящей связи от которых актор согласен.
Определение 3 [3]. Пусть множества действий игроков таковы, что из того, что актор i может иметь или не иметь предложение к актору j, следует, что актор j может принять, а может и не принять это предложение. Тогда будем говорить, что в сетевой игре для образования связи требуется согласие обоих игроков. Игры, в которых для образования связи требуется согласие обоих акторов, называются играми согласия.
Поскольку нас интересуют не действия акторов, а формируемые в результате этих действий оптимальные в некотором смысле структуры (союзы государств, конфедерации, федерации и т.д.), то далее будем рассматривать только игры согласия. Игры, в которых для образования связи требуется желание одного игрока, обычно рассматриваются в военно-политических приложениях.
Определение 4. Коалицией (социально-политической коалицией), формируемой актором i (принципалом коалиции), называется ориентированное дерево единичной высоты 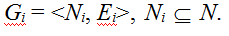 Принципал является корнем дерева, другие акторы, входящие в коалицию (агенты), –листьями дерева. Любой актор может входить только в одну коалицию, или ни в какую коалицию не входить. Принципал является корнем дерева, другие акторы, входящие в коалицию (агенты), –листьями дерева. Любой актор может входить только в одну коалицию, или ни в какую коалицию не входить.
Определение 5. Коалиция Gi называется однородной, если для всех агентов коалиции степень их интеграции с принципалом одинакова 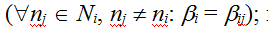 иначе коалиция называется неоднородной. иначе коалиция называется неоднородной.
Множество коалиций, формируемых принципалами 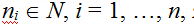 является лесом. является лесом.
Определение 6. Коалиция Gi называется допустимой, если между принципалом и любым его агентом на географическом графе существует путь между ними, проходящий через вершины входящих в коалицию агентов.
На рис. 7 показана допустимая коалиция, формируемая 1-м актором, а на рис. 8 – недопустимая.

Рис. 7. Допустимая коалиция, формируемая 1-м актором на географическом графе

Рис. 8. Недопустимая коалиция, формируемая 1-м актором на географическом графе
В первом случае в коалицию входят акторы 1 (принципал), 2, 3, 4 и 6. Между принципалом и любым агентом на географическом графе существует путь, проходящий через вершины, входящие в коалицию.
Во втором случае коалиция недопустима, поскольку на географическом графе нет пути между акторами 1 и 4 (актор 3 не входит в коалицию).
Проверку на допустимость тех или иных коалиций можно выполнять с использованием матрицы смежностей h географического графа и построением матрицы достижимости.
Если не оговорено иное, далее будем рассматривать только допустимые коалиции.
Пусть 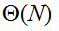 – множество всех допустимых коалиций с множеством вершин N. Заинтересованность акторов в той или иной коалиции можно описать функциями выигрыша – множество всех допустимых коалиций с множеством вершин N. Заинтересованность акторов в той или иной коалиции можно описать функциями выигрыша 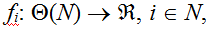 каждая из которых определяет выигрыш i-го актора при реализации различных коалиций. Таким образом, в модель организации коалиций входят множество акторов N = {1, …, n}, географический граф H и набор функций выигрыша каждая из которых определяет выигрыш i-го актора при реализации различных коалиций. Таким образом, в модель организации коалиций входят множество акторов N = {1, …, n}, географический граф H и набор функций выигрыша 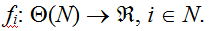
Рассмотрим географический граф, показанный на рис. 9. Вершинами показанного на рисунке географического графа, например, могут быть: 1 – Германия, 2 – Польша, 3 – Словакия, 4 – Литва. Из этих стран Польша имеет сухопутную границу со всеми остальными.

Рис. 9. Географический граф (четыре политических актора, ребра – наличие границ между ними)
Допустимыми коалициями на графе H являются следующие коалиции (множество 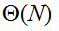 ): ):
1) (1, 2, 3, 4) – пустой граф G;
2) (1–2, 3, 4) – коалиция акторов 1 и 2;
3) (1–2–3, 4) – коалиция акторов 1, 2 и 3;
4) (1–2–3–4) – коалиция акторов 1, 2, 3 и 4;
5) (1, 2–3, 4) – коалиция акторов 2 и 3;
6) (1, 2–4, 3) – коалиция акторов 2 и 4;
7) (1, 2–3–4) – коалиция акторов 2, 3 и 4.
Определение 7. Сетевые игры согласия на географическом графе H называются сетевыми играми безопасности социально-политических акторов, если целевыми функциями акторов являются функции безопасности.
Сетевая игра безопасности определена, если заданы:
1) Множество акторов N = {1, …, n}.
2) Географический граф H.
3) Набор функций выигрыша на множестве всех допустимых коалиций 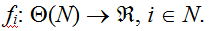
4) Правило формирования коалиций (выбора акторами стратегий).
Пусть  есть множество всех допустимых коалиций (включая коалицию, состоящую из одного актора), в которых актор i является принципалом. Очевидно, что выполняется условие: есть множество всех допустимых коалиций (включая коалицию, состоящую из одного актора), в которых актор i является принципалом. Очевидно, что выполняется условие:
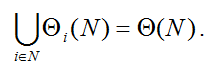
Для каждой коалиции 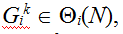 управляя вектором связей управляя вектором связей 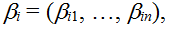 где где 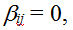 если актор j не входит в коалицию, и если актор j не входит в коалицию, и 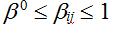 иначе, вычисляется максимальное значение функции безопасности: иначе, вычисляется максимальное значение функции безопасности:
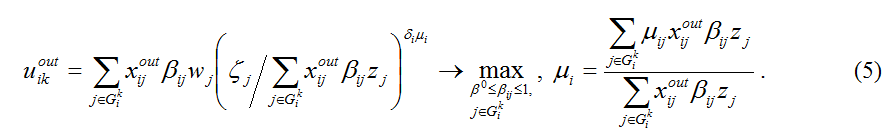
В результате решения задачи (5) находится оптимальный вектор 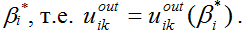  . .
Пример 1. Для географического графа, показанного на рис. 9, функции безопасности коалиций представлены в виде матрицы U размера mхn, где m – количество допустимых коалиций:

Для указанных коалиций матрицы предложений акторов равны (номер строки – номер актора, делающего предложение, номер столбца – номер актора, кому делается предложение):
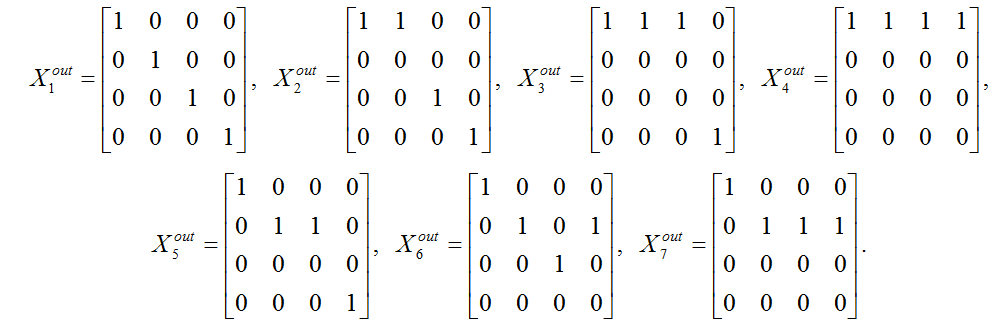
Матрицы согласий получаются путем транспонирования матриц предложений, т.е. Xink=(Xoutk)T, k = 1, …, m. Например, для 7-й коалиции матрица согласий равна:
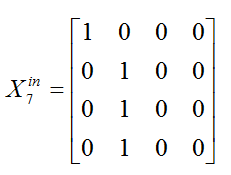
(первый актор получает предложение от себя, второй, третий и четвертый – от второго).
В дополнение к матрице U функций безопасности коалиций определим матрицу Y коалиций размера mxn по следующему правилу:
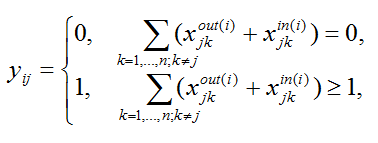
где: xout(i)jk – элемент в j-й строке и k-м столбце матрицы Xouti, xin(i)jk – элемент в j-й строке и k-м столбце матрицы Xini. Суммирование выполняется по всем элементам j-й строки матрицы Xouti+Xini, кроме диагональных.
Для матрицы U получим следующую матрицу Y:
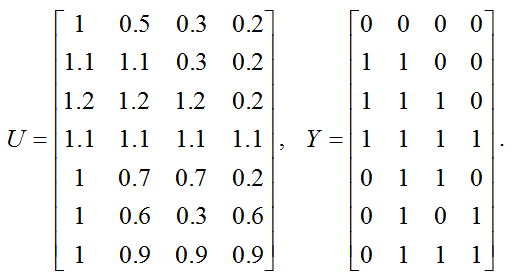
Для i-й коалиции (строки матрицы Y) значения элемента yij равно 1, если актор j входит в некоторую коалицию, состоящую из двух или более акторов.
4. Сетевые игры безопасности социально-политических акторов
Имея игровую матрицу U размера mxn, i-й актор 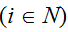 выбирает действие xi = j, т.е. j-ю коалицию, j = 1, …, m. Выбор действий акторами осуществляется однократно, одновременно и независимо. выбирает действие xi = j, т.е. j-ю коалицию, j = 1, …, m. Выбор действий акторами осуществляется однократно, одновременно и независимо.
Выигрыш i-го актора зависит от его собственного действия и вектора действий оппонентов (обстановки игры) x-i = (x1, …, xi-1, xi+1, …, xn). Профиль действий акторов складывается из действия i-го актора и обстановки игры, т.е. x = (xi, xi-1).
Профиль действий x* акторов называется равновесием Нэша, если для любого игрока и любого его действия справедливо [3]:
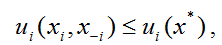 (6) (6)
где ui(.) – значение функции безопасности коалиции, в которую входит актор i.
Пример 2. Найти равновесие Нэша по игровой матрице из примера 1.
Первый актор может получить максимально возможный выигрыш (равный 1.2), выбирая 3-ю коалицию, состоящую из акторов 1, 2 и 3. Эта коалиция выгодна акторам 2 и 3, поскольку выбирая любую другую коалицию, они получат меньший выигрыш. И в тоже время формирование данной коалиции не зависит от действий актора 4.
Следовательно, оптимальной по Нэшу будет коалиция, показанная на рис. 10.
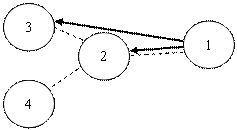
Рис. 10. Оптимальная по Нэшу коалиция
Имея модель сетевой игры безопасности, далее рассмотрим задачи управления интеграцией и дезинтеграцией сетевых структур на примере Евросоюза.
5. Управление интеграцией и дезинтеграцией сетевых структур
В ходе интеграционных процессов в Центральной и Западной Европе одновременно идут и дезинтеграционные. В 1991–2008 гг. произошли события, связанные с распадом федеративной Югославии. В 1993 г. Чехословакия разделилась на самостоятельные государства – Чехию и Словакию, вошедшие в 2004 г. в Европейский Союз. В 1992 г. жители Швейцарской Конфедерации на референдуме высказались против присоединения их страны к Европейскому экономическому пространству. В 2016 г. население Великобритании проголосовало за выход из Евросоюза. В 2017 г. за независимость от Испании проголосовало 90 % жителей Каталонии (при явке 43 %).
Любое государство выполняет ряд функций (правовую, политическую, социальную, культурную, образовательную, национальной безопасности и обороны и др.). Когда межгосударственное образование (Европейское экономическое пространство, Европейский Союз) начинает трансформироваться в надгосударственное образование (конфедерацию, федерацию), его функции распространяются на все административные (этнические) образования входящих в него государств. В результате функции государства начинают дублируются. Выходов из данной ситуации несколько: выход полиэтнического государства из Союза, отказ от дальнейшей интеграции, распад государства и вхождение его частей в Союз.
Рассмотрим модель сетевой структуры с географическим графом, показанным на рис. 11.
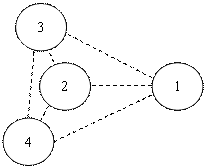
Рис. 11. Географический граф (вершины – акторы, ребра – границы между ними)
Пусть актор 1 – это крупное союзное образование, актор 2 – этнический центр федерации, акторы 3 и 4 – субъекты федерации.
Если Союз имеет межгосударственный характер, то допустима только одна коалиция, показанная на рис. 12.
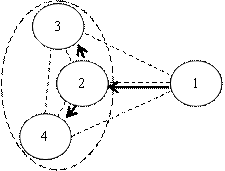
Рис. 12. Коалиция при межгосударственном Союзе (вершины – политические акторы, ребра – границы и политические связи между ними)
Вычислим функции безопасности акторов и коалиций при исходных данных, указанных в таблице 3.
Таблица 3. Исходные данные для расчета функции безопасности
|
№
|
Показатель
|
Значения показателя для акторов
|
|
1
|
2
|
3
|
4
|
|
1
|
Численность населения, zi
|
200
|
20
|
5
|
3
|
|
2
|
Значение функции развития, wi
|
0,06
|
0,02
|
0,006
|
0,003
|
|
3
|
Численность титульного этноса, 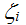
|
80
|
20
|
5
|
3
|
|
4
|
Параметр притяжения, 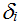
|
0,5
|
0,5
|
|
|
Значения параметра разнородности заданы симметричной матрицей M с элементами 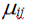 : :
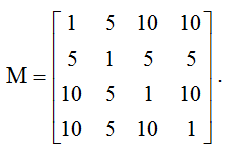
Федерация, образованная актором 2, характеризуется следующими параметрами интеграции: 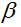 23 = 0,75, 23 = 0,75, 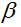 24 = 0,75. Параметр интеграции Союза равен 24 = 0,75. Параметр интеграции Союза равен 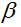 12 = 0,15. 12 = 0,15.
Результаты расчетов представлены в таблице 4.
Таблица 4. Результаты расчета функций безопасности
|
№
|
Показатель
|
Значение
|
|
1
|
Функция безопасности актора 2
|
0,020
|
|
2
|
Функция безопасности федерации (2–3–4)
|
0,021
|
|
3
|
Функция безопасности актора 1
|
0,0379
|
|
4
|
Функция безопасности Союза (1–2)
|
0,0380
|
Из результатов расчетов следует, что вхождение федерации в Союз выгодно обоим акторам.
При различных значениях параметра притяжения актора 1 (1,0, 0,5 и 0,3) вычислены значения функции безопасности Союза в зависимости от параметра интеграции (рис. 13).
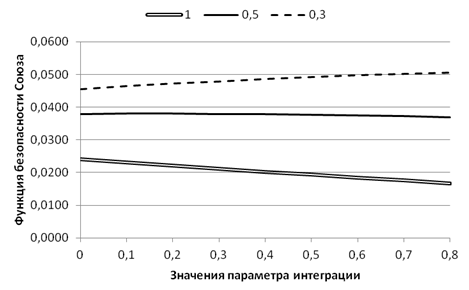
Рис. 13. Зависимость функции безопасности Союза от параметра интеграции (от доли государственных функций, переданных в ведение Союза)
На рис. 14 показана коалиция, формируемая надгосударственным Союзом.
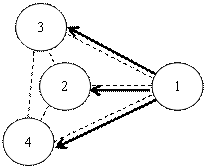
Рис. 14. Коалиция при надгосударственном Союзе (вершины – политические акторы, пунктирные ребра – границы между ними, сплошные ребра – социально-политические связи)
При значениях параметров интеграции 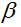 12 = 12 = 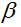 13 = 13 = 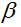 14 = 0,15 и при 14 = 0,15 и при 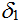 = 0,5 значение функции безопасности надгосударственного союза равно 0.0382. То есть надгосударственный Союз в рассматриваемом случае эффективнее Союза межгосударственного для всех акторов. = 0,5 значение функции безопасности надгосударственного союза равно 0.0382. То есть надгосударственный Союз в рассматриваемом случае эффективнее Союза межгосударственного для всех акторов.
При различных значениях параметра притяжения актора 1 (1,0, 0,5 и 0,3) вычислены значения функции безопасности надгосударственного Союза в зависимости от параметра интеграции (рис. 15).
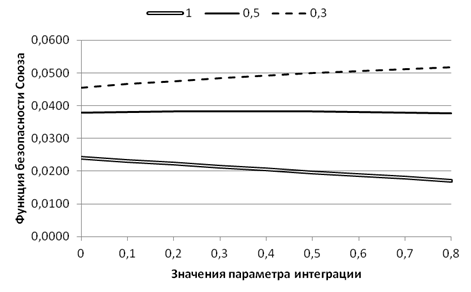
Рис. 15. Зависимость функции безопасности надгосударственного Союза от параметра интеграции (от доли государственных функций, переданных в ведение Союза)
Из результатов расчетов видно, что при низких интеграционных возможностях первого актора (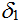 = 1) с ростом степени интеграции политических акторов функция безопасности Союза понижается. Соответственно при = 1) с ростом степени интеграции политических акторов функция безопасности Союза понижается. Соответственно при 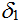 = 0,3 функция безопасности Союза увеличивается (интеграция выгодна). = 0,3 функция безопасности Союза увеличивается (интеграция выгодна).
Таким образом, состав и структура социально-политических коалиций в значительной степени определяются возможностями политических акторов объединять и сплачивать различные народы и этносы для решения общих дел (параметр притяжения) и существующими межэтническими гетерогенностями (оцениваются параметром разнородности). В силу сложности оценки названных параметров, в научной и политической сферах обычно используют представления о них – субъективные оценки и предпочтения, отражаемые в общественно-политическом сознании («еврооптимисты» и «евроскептики» и т.д.). Поэтому актуальной и важной представляется задача социально-информационного управления процессами интеграции и дезинтеграции политических акторов.
6. Заключение
Степень национальной безопасности государства является интегрированным показателем, учитывающим возможности государства и общества по устойчивому развитию, повышению уровня жизни граждан и обеспечению их защищенности. Представленная модель безопасности позволяет количественно оценить степень национальной безопасности государств, используя ограниченный список показателей (численность населения, площадь занимаемой территории, этнический состав населения и др.). Параметры модели оценены на исторических данных.
Поскольку безопасность государств оценивается не только исследователями, но и тысячами и миллионами граждан, мигрирующих из одних регионов (государств) в другие в поисках лучших условий жизни и безопасного проживания, то для верификации модели безопасности использовались данные по региональной и международной миграции.
Функция безопасности государства (над- и межгосударственного образования) состоит из двух компонент: функции развития и функции сохранения. При увеличении числа входящих в Союз государств увеличивается совокупный размер валового внутреннего продукта, суммарная численность вооруженных сил и другие показатели. Вместе с тем снижаются возможности по оперативному согласованию множества противоречивых интересов правительств и народов отдельных государств, обусловленных культурными и этническими разнородностями. Модель безопасности и расчеты с ее использованием объясняют ситуацию, когда Евросоюз, обладая высоким совокупным потенциалом отдельных стран (500 миллионов человек населения, 23% мирового ВВП), имеет крайне низкую политическую субъектность, находясь в зависимости в военно-политическом отношении от США.
Расчеты показывают, что в существующем ныне составе Европейский Союз является неустойчивым объединением и не сможет перейти к федеративному устройству. В этой связи представляется актуальным и важным исследование проблемы формирования устойчивых в том или ином смысле социально-политических над- и межгосударственных образований. Причем эта проблема актуальна не только для стран Европейского Союза, но и для других образований (Евразийский экономический союз и т.д.).
Для научного решения указанной проблемы автором разработана сетевая теоретико-игровая модель безопасности, предназначенная для поиска устойчивых социально-политических образований. В сетевой модели безопасности рассматриваются два графа: географический граф – отражающий существующие между государствами границы, и социально-политический граф, дуги которого интерпретируются как наличие социально-политической связи между вершинами (государствами). Модель организации сетевых структур (множество акторов и их функций выигрыша) дополнена правилом формирования структур: акторы входят в некоторую коалицию, если при этом повышается ее безопасность.
С использованием сетевой модели можно приступить к решению актуальной задачи государственной пограничной политики – созданию системы мониторинга геополитических процессов и их влияния на формирование угроз национальной безопасности Российской Федерации в пограничном пространстве.
Решена частная научная задача управления интеграцией и дезинтеграцией сетевых социально-политических структур и в терминах теории безопасности объяснены успешно идущие процессы интеграции мононациональных стран в единый Союз и связанные с ними процессы дезинтеграции многонациональных государств (или их отказа от дальнейшей интеграции).
Степень интеграции государств завис как от объективных (численности населения, этнический состав), так и от субъективных (предпочтения политических партий и групп) факторов. Имея модель формирования социально-политических коалиций, можно ставить и решать теоретико-игровые задачи управления формированием меж- и наднациональных союзов (сетевые игры безопасности).
Библиография
1. Аберкромби Н., Хилл С., Тернер Б. Социологический Словарь. 2-е изд., перераб. и доп. / Пер. с англ. И.Г. Ясавеева, под ред. С.А.Ерофеева. – М.: Экономика, 2004. – 620 с.
2. Военная доктрина Российской Федерации. – Утверждена Президентом Российской Федера-ции 25.12.2014 N Пр-2976.
3. Губко М. В. Управление организационными системами с сетевым взаимодействием агентов. I. Обзор теории сетевых игр // Автоматика и телемеханика. – 2004. – № 8. – с. 115–132.
4. Макиавелли Н. Государь. – М.: Планета, 1990. – 80 с.
5. Основы государственной пограничной политики Российской Федерации (проект). – URL: http://www.fsb.ru/files/PDF/Osnovy_proekt.pdf (дата обращения: 10.04.2018).
6. Сороко Е. Этнически смешанные супружеские пары в Российской Федерации // Демогра-фическое обозрение. – 2014. – Т. 1. – № 4. – С. 96–123.
7. Тельнова Н.А. Основные принципы синергетики и их методологическое значение // Вестник ВолГУ. Серия 7: Философия. Социология и социальные технологии. – 2006. – № 5. – С. 14–20.
8. Шумов В.В. Государственная и общественная безопасность: Моделирование и прогнозиро-вание. – М.: ЛЕНАНД, 2016. – 144 с.
9. Alesina A., Spolaore E. War, Peace and the Size of Countries // Journal of Public Economics. – 2005. – № 89 (7). – P. 1333-1354.
10. Maddison Historical Statistics [Электронный ресурс]. – URL: https://www.rug.nl/ggdc/historicaldevelopment/maddison/ (дата обращения: 23.01.2018).
References
1. Aberkrombi N., Khill S., Terner B. Sotsiologicheskii Slovar'. 2-e izd., pererab. i dop. / Per. s angl. I.G. Yasaveeva, pod red. S.A.Erofeeva. – M.: Ekonomika, 2004. – 620 s.
2. Voennaya doktrina Rossiiskoi Federatsii. – Utverzhdena Prezidentom Rossiiskoi Federa-tsii 25.12.2014 N Pr-2976.
3. Gubko M. V. Upravlenie organizatsionnymi sistemami s setevym vzaimodeistviem agentov. I. Obzor teorii setevykh igr // Avtomatika i telemekhanika. – 2004. – № 8. – s. 115–132.
4. Makiavelli N. Gosudar'. – M.: Planeta, 1990. – 80 s.
5. Osnovy gosudarstvennoi pogranichnoi politiki Rossiiskoi Federatsii (proekt). – URL: http://www.fsb.ru/files/PDF/Osnovy_proekt.pdf (data obrashcheniya: 10.04.2018).
6. Soroko E. Etnicheski smeshannye supruzheskie pary v Rossiiskoi Federatsii // Demogra-ficheskoe obozrenie. – 2014. – T. 1. – № 4. – S. 96–123.
7. Tel'nova N.A. Osnovnye printsipy sinergetiki i ikh metodologicheskoe znachenie // Vestnik VolGU. Seriya 7: Filosofiya. Sotsiologiya i sotsial'nye tekhnologii. – 2006. – № 5. – S. 14–20.
8. Shumov V.V. Gosudarstvennaya i obshchestvennaya bezopasnost': Modelirovanie i prognoziro-vanie. – M.: LENAND, 2016. – 144 s.
9. Alesina A., Spolaore E. War, Peace and the Size of Countries // Journal of Public Economics. – 2005. – № 89 (7). – P. 1333-1354.
10. Maddison Historical Statistics [Elektronnyi resurs]. – URL: https://www.rug.nl/ggdc/historicaldevelopment/maddison/ (data obrashcheniya: 23.01.2018).
|


















 Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
 Рус
Рус



