Неоднозначность результатов при использовании методов класса Parallel в рамках исполняющей среды .NET Framework

Введение

В научных и инженерных расчетах точность является важным критерием, определяющим достоверность результатов. При проведении математических операций и вычислений на ЭВМ (электронно-вычислительной машине) возникает необходимость округления чисел, что может приводить к погрешностям. Поэтому снижение погрешности расчетов, связанной с использованием округлений, является важной задачей в научной и инженерной практике.

Округление чисел происходит в результате ограничения количества значащих цифр после запятой, что неизбежно приводит к потере точности. В зависимости от задачи и требуемой точности необходимо выбирать правильный способ округления чисел. Например, при округлении до целого числа, некоторые десятичные дроби будут потеряны, а при округлении до определенного числа знаков после запятой произойдет потеря точности из-за отбрасывания оставшихся десятичных цифр.

Снижение погрешности расчетов может быть достигнуто путем использования более точных методов вычислений, таких как метод Гаусса или методы численного интегрирования. Кроме того, для уменьшения погрешности можно применять различные алгоритмы и техники вычислений, которые позволяют уменьшить потерю точности при округлении чисел.

Снижение погрешности расчетов особенно важно в случаях, когда требуется высокая точность, например, при использовании методов решения систем линейных уравнений ^[1], при использовании численных методов дифференцирования и интегрирования ^[2], при моделировании физических явлений ^[3], при вычислении математических функций ^[4], при вычислении процентных ставок или доходности инвестиций ^[5,6], при использовании алгоритмов машинного обучения и искусственного интеллекта ^[7]. В этих случаях даже небольшие погрешности могут привести к серьезным ошибкам и неверным результатам, которые могут негативно повлиять на принимаемые решения.

Таким образом, снижение погрешности расчетов, связанной с использованием округлений, является важным фактором в научной и инженерной практике, поскольку позволяет получать более точные результаты вычислений и уменьшить вероятность ошибок и неверных выводов.

В современных вычислительных системах все более широко используются технологии параллельного программирования для увеличения производительности. Однако при использовании параллельных алгоритмов возникают дополнительные сложности ^[8,9], связанные с необходимостью обмена данными между различными процессами, а также с синхронизацией операций.

В условиях параллельного программирования использование округления чисел может приводить к возникновению дополнительных погрешностей, связанных с несогласованностью округления между различными процессами. Это может приводить к ошибкам в вычислениях, что особенно важно в случаях, когда требуется высокая точность вычислений.

Поэтому снижение погрешности расчетов, связанной с использованием округлений, имеет практическую значимость в технологиях параллельного программирования. Для уменьшения погрешностей в параллельных алгоритмах необходимо применять специальные алгоритмы и техники. В частности, это актуально в ходе параллельного агрегирования локальных значений, что определяет предмет исследования данной статьи. В демонстрационных целях взята задача – вычисление квадратных корней, которое часто используется в различных областях науки и техники, где необходимы точные вычисления.

Вычисление суммы квадратных корней может быть полезным в решении многих задач, таких как:

• Определение расстояния между двумя точками в n-мерном пространстве.
• Вычисление нормы вектора в n-мерном пространстве.
• Расчет площади кривой на плоскости.
• Определение времени, за которое тело падает на землю с заданной высоты при ускорении свободного падения.
• Расчет стоимости доставки груза в зависимости от расстояния и веса груза.
• Определение времени, за которое свет проходит расстояние между двумя точками в пространстве.
• Оценка времени, необходимого для прохождения тестов и обучения в машинном обучении.
• Оценка скорости работы компьютерных программ и алгоритмов.

Неоднозначность результатов в ходе параллельной агрегации локальных значений

Методы Parallel.For и Parallel.ForEach предлагают набор перегруженных версий, которые работают с аргументом обобщенного типа по имени TLocal. Такие перегруженные версии призваны помочь оптимизировать объединение данных из циклов с интенсивными итерациями. Ниже представлена перегруженная версия метода Parallel.For, которую далее мы будем использовать в предметном анализе.

public static ParallelLoopResult For(

ᅠint fromInclusive,

ᅠint toExclusive,

ᅠFunc localInit,

ᅠFunc<int, ParallelLoopState, TLocal, TLocal> body,

ᅠAction localFinally);

Где:

• fromInclusive – начальный индекс, включительно.
• toExclusive – конечный индекс, не включительно.
• localInit – делегат функции, который возвращает начальное состояние локальных данных для каждой задачи.
• body – делегат, который вызывается один раз за итерацию.
• localFinally – делегат, который выполняет финальное действие с локальным результатом каждой задачи.
• TLocal – тип данных, локальных для потока.
• Возвращаемый объект – структура (ParallelLoopResult), в которой содержатся сведения о выполненной части цикла.

Применим данный метод на практике, чтобы просуммировать квадратные корни чисел от 1 до 10⁷.

object locker = new object();

double grandTotal = 0;

Parallel.For(1, 10000000,

ᅠ() => 0.0, // Initialize the local value.

ᅠ(i, state, localTotal) => // Body delegate. Notice that it

ᅠᅠlocalTotal + Math.Sqrt(i), // returns the new local total.

ᅠlocalTotal => // Add the local

ᅠᅠ{ lock (locker) grandTotal += localTotal; } // to the master value.

);

Console.WriteLine(grandTotal);

Данное решение может выдавать неоднозначный результат, например:

• 21081849486,4431;
• 21081849486,4428;
• 21081849486,4429.

Таким образом, по итогам запусков программы результаты вычислений могут отличаться в 3 или 4 знаке после запятой, что является недопустимым при решении таких задач, как:

• Научные и инженерные расчеты, связанные с проектированием и тестированием новых технологий и устройств, где даже небольшие погрешности могут привести к неправильным выводам.
• Разработка и анализ финансовых моделей, где точность результатов может оказать значительное влияние на принимаемые инвестиционные решения.
• Работа с большими наборами данных в машинном обучении и анализе данных, где точность результатов может быть важна для получения правильных выводов и прогнозов.
• Вычисление физических и химических констант, таких как постоянная Планка или постоянная Больцмана, которые используются в широком диапазоне научных и инженерных расчетов.
• Исследования в области астрономии и космологии, где высокая точность результатов может быть важна для определения физических характеристик звезд, планет и галактик.

Причина неоднозначности результатов является комплексной. Во-первых, имеют место ошибки округления вещественных чисел. Во-вторых, выполнение делегата, отвечающего за формирование локального накопителя, в потоках пула носит порциональный характер. Рассмотрим и то и другое более детально.

Типы float и double внутренне представляют числа в двоичной форме. По указанной причине точно представляются только числа, которые могут быть выражены в двоичной системе счисления. На практике это означает, что большинство литералов с дробной частью (которые являются десятичными) не будут представлены точно. Например:

float x = 0.1f; // Не точно 0.1

Console.WriteLine (x + x + x + x + x + x + x + x + x + x); // 1.0000001

Именно потому типы float и double не подходят для финансовых вычислений. В противоположность им тип decimal работает в десятичной системе счисления, так что он способен точно представлять дробные числа вроде 0.1, выразимые в десятичной системе (а также в системах счисления с основаниями-множителями 10 – двоичной и пятеричной). Поскольку вещественные литералы являются десятичными, тип decimal может точно представлять такие числа, как 0.1. Тем не менее, ни double, ни decimal не могут точно представлять дробное число с периодическим десятичным представлением:

decimal m = 1M / 6M; // 0.1666666666666666666666666667M

double d = 1.0 / 6.0; // 0.16666666666666666

Это приводит к накапливающимся ошибкам округления:

decimal notQuiteWholeM = m+m+m+m+m+m; // 1.0000000000000000000000000002M

double notQuiteWholeD = d+d+d+d+d+d; // 0.99999999999999989

которые нарушают работу операций эквивалентности и сравнения:

Console.WriteLine (notQuiteWholeM == 1M); // False

Console.WriteLine (notQuiteWholeD < 1.0); // True

Ниже в таблице 1 представлен обзор отличий между типами double и decimal.

Таблица 1. Отличия между типами double и decimal ^[9]

Раскроем тип decimal более детально, чтобы ответить на вопрос, почему обработка данных типа decimal не является присущей процессору.

Двоичное представление decimal числа состоит из 1-битового знака, 96-битового целого числа и коэффициента масштабирования, используемого для деления целочисленного числа и указания его части десятичной дроби. Коэффициент масштабирования неявно представляет собой число 10, возведенное в степень в диапазоне от 0 до 28. Таким образом, bits – это массив из четырех элементов, состоящий из 32-разрядных целых чисел со знаком:

• bits_0, bits_1 и bits_2 содержат низкие, средние и высокие 32 биты 96-разрядного целого числа.
• bits_3:
  • 0-15 не используются;
  • 16-23 (8 бит) содержат экспоненту от 0 до 28, что указывает на степень 10 для деления целочисленного числа;
  • 24-30 не используются;
  • 31 содержит знак (0 означает положительное значение, а 1 – отрицательное).

Для вычисления суммы квадратных корней с использованием типа данных decimal некоторые параметры представления числа, которые могут быть значимыми, включают:

• Количество знаков в дробной части – чем больше знаков, тем точнее будет представление квадратных корней, и тем выше точность вычисления суммы.
• Режим округления – если результат вычисления имеет много знаков после запятой, режим округления может повлиять на точность вычисления суммы. Режим округления может влиять на округление до ближайшего четного числа или до ближайшего нечетного числа, что может повлиять на точность.
• Размер памяти – чем больше размер памяти, тем больше знаков можно хранить, и тем выше точность вычисления суммы.
• Диапазон значений – это может быть не столь значимо, так как в задаче вычисления суммы квадратных корней используются только положительные значения.

В целом, для вычисления суммы квадратных корней с использованием типа данных decimal, параметры, которые являются наиболее значимыми, это количество знаков в дробной части и режим округления. Эти параметры могут быть выбраны на основе требуемой точности и скорости выполнения вычислений.

Разбиение на основе порций работает путем предоставления каждому рабочему потоку возможности периодически захватывать из входной последовательности небольшие “порции” элементов с целью их обработки ^[9]. Например (рис. 1), инфраструктура Parallel LINQ начинает с выделения очень маленьких порций (один или два элемента за раз) и затем по мере продвижения запроса увеличивает размер порции: это гарантирует, что небольшие последовательности будут эффективно распараллеливаться, а крупные последовательности не приведут к чрезмерным циклам полного обмена. Если рабочий поток получает “простые” элементы (которые обрабатываются быстро), то в конечном итоге он сможет получить больше порций. Такая система сохраняет каждый поток одинаково занятым (а процессорные ядра “сбалансированными”); единственный недостаток состоит в том, что извлечение элементов из разделяемой входной последовательности требует синхронизации – и в результате могут появиться некоторые накладные расходы и состязания.

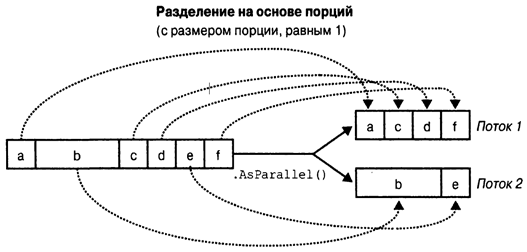
Рисунок 1. Разделение на основе порций ^[9]

Метод For класса Parallel работает схожим образом, разница лишь в том, что вместо элемента входной последовательности выступает номер итерации, который как правило учитывается при выполнении тела цикла (точнее делегата типа Action). Реализация разделения основана на механизме разбиения на порции, при котором размер порции потенциально увеличивается в случае положительной динамики обработки итераций. Такой подход помогает обеспечить качественную балансировку нагрузки при небольшом количестве итераций и минимизировать число монопольных блокировок (в ходе назначения диапазонов номеров итераций для рабочих потоков) при их большом количестве. При этом обеспечивается, чтобы большинство итераций потока было сосредоточено в одной и той же области итерационного пространства для достижения высокой локальности кэша.

Исследование метода Parallel.For для детализации причины неоднозначности конечного результата

Реализация метода For сложна и требует детального рассмотрения, которое выходит за рамки данной статьи. Тем не менее отметим некоторые моменты программной реализации метода Parallel.For с аргументом обобщенного типа.

public static ParallelLoopResult For (int fromInclusive, int toExclusive, Func localInit, Func <int, ParallelLoopState, TLocal, TLocal> body, …) {

ᅠ…

ᅠreturn ForWorker(fromInclusive, toExclusive, s_defaultParallelOptions,

ᅠᅠnull, null, body, localInit, localFinally);

}

private static ParallelLoopResult ForWorker (int fromInclusive, int toExclusive, ParallelOptions parallelOptions, Action body, …) {

ᅠ…

ᅠrootTask = new ParallelForReplicatingTask(parallelOptions, delegate {

ᅠᅠif (rangeWorker.FindNewWork32(

ᅠᅠᅠᅠout var nFromInclusiveLocal,

ᅠᅠᅠᅠout var nToExclusiveLocal) &&

ᅠᅠᅠᅠ!sharedPStateFlags.ShouldExitLoop(nFromInclusiveLocal)) {

ᅠᅠᅠᅠ…

ᅠᅠᅠᅠdo {

ᅠᅠᅠᅠᅠif (body != null) {

ᅠᅠᅠᅠᅠᅠfor (int i = nFromInclusiveLocal; i < nToExclusiveLocal; i++) {

ᅠᅠᅠᅠᅠᅠᅠif (sharedPStateFlags.LoopStateFlags != ParallelLoopStateFlags.PLS_NONE

ᅠᅠᅠᅠᅠᅠᅠᅠ&& sharedPStateFlags.ShouldExitLoop()) {

ᅠᅠᅠᅠᅠᅠᅠᅠbreak;

ᅠᅠᅠᅠᅠᅠᅠ}

ᅠᅠᅠᅠᅠᅠᅠbody(i);

ᅠᅠᅠᅠᅠᅠ}

ᅠᅠᅠᅠᅠ}

ᅠᅠᅠᅠ}

ᅠᅠᅠᅠwhile (rangeWorker.FindNewWork32(out nFromInclusiveLocal, out nToExclusiveLocal) …);

ᅠᅠᅠᅠ…

ᅠᅠ}

ᅠ}, creationOptions, internalOptions);

ᅠrootTask.RunSynchronously(parallelOptions.EffectiveTaskScheduler);

ᅠrootTask.Wait();

ᅠ…

}

internal ParallelForReplicatingTask(...) {

ᅠm_replicationDownCount = parallelOptions.EffectiveMaxConcurrencyLevel;

ᅠ…

}

Метод rootTask.RunSynchronously запускает исполнение задач в рабочих потоках пула, при этом число задач задается свойством parallelOptions.EffectiveMaxConcurrencyLevel. Метод FindNewWork32 определяет рабочий диапазон для каждого потока пула. В представленном коде можно увидеть, что выполнение любой задачи не ограничивается выполнением первоначально определенного диапазона, потоки пула продолжают работу для вновь задаваемых диапазонов в операторе while.

Проведем детализацию работы метода Parallel.For с аргументом обобщенного типа на ранее представленном примере по суммированию квадратных корней чисел, расширив код следующим образом.

object locker = new object();

double grandTotal = 0;

ConcurrentBag<(int?, double)> cb1 = new ConcurrentBag<(int?, double)>();

ConcurrentDictionary<int?, long> cd = new ConcurrentDictionary<int?, long>();

ConcurrentBag<(int?, int)> cb2 = new ConcurrentBag<(int?, int)>();

var time = Stopwatch.StartNew();

time.Start();

Parallel.For(1, 1000,

ᅠ() => { return 0.0; },

ᅠ(i, state, localTotal) =>

ᅠ{

ᅠᅠcb1.Add((Task.CurrentId, localTotal));

ᅠᅠif (!cd.ContainsKey(Task.CurrentId)) cd[Task.CurrentId] = time.ElapsedTicks;

ᅠᅠcb2.Add((Task.CurrentId, i));

ᅠᅠreturn localTotal + Math.Sqrt(i);

ᅠ},

ᅠlocalTotal =>

ᅠ{ lock (locker) grandTotal += localTotal; }

);

cb1.GroupBy(_ => _.Item1).Select(_ => new

{

ᅠTaskId = _.Key,

ᅠIterations = _.Count(),

ᅠStartTime = cd[_.Key]

}).OrderBy(_ => _.StartTime).Dump();

var query = cb2.OrderBy(_ => _.Item2).GroupBy(_ => _.Item1, _ => _.Item2);

foreach (var grouping in query)

{

ᅠConsole.WriteLine("TaskId: " + grouping.Key);

ᅠvar r = grouping.GetEnumerator();

ᅠint? i = null;

ᅠbool onlyOne = true;

ᅠforeach (int iteration in grouping)

ᅠ{

ᅠᅠif (i == null)

ᅠᅠᅠConsole.Write("{" + $"{iteration}");

ᅠᅠelse

ᅠᅠ{

ᅠᅠᅠif (iteration - i != 1)

ᅠᅠᅠᅠConsole.Write(",...," + i + "}, {" + iteration);

ᅠᅠᅠonlyOne = false;

ᅠᅠ}

ᅠᅠi = iteration;

ᅠ}

ᅠif (onlyOne) Console.WriteLine("}");

ᅠelse Console.WriteLine(",...," + i + "}");

}

Программный код позволяет учесть:

• идентификатор каждой задачи TaskId;
• количество итераций выполненное в рамках каждой задачи Iterations;
• StartTime – время начала работы каждой задачи, выраженное в тиках посредством класса Stopwatch (один тик является меньше одной микросекунды);
• диапазоны номеров обработанных итераций каждой задачи.

Например, по результатам работы программы на машине, способной выполнять 8 потоков параллельно на аппаратном уровне, можно получить следующие показатели TaskId, Iterations, StartTime (табл. 2). Диапазоны номеров обработанных итераций представлены в таблице 3.

Таблица 2. Показатели TaskId, Iterations, StartTimeпосле завершения метода Parallel.For

Таблица 3. Диапазоны номеров обработанных итераций каждой задачи

По результатам работы программы можно увидеть, что рабочие диапазоны различны. Некоторые задачи состоят из единственной итерации. Но это не является недостатком алгоритма по которому реализован исследуемый метод, а следствием того, что обработка одной итерации представляет собой нетрудоемкую с вычислительной точки зрения процедуры. Так, например, если в целевой метод делегата, представляющий четвертый параметр метода Parallel.For, добавить строки:

for (int k = 0; k < 1000000; k++)

ᅠMath.Sqrt(k);

тем самым существенно усложнив обработку каждой итерации цикла, то можно получить равномерное распределение диапазонов по задачам (табл. 4).

Таблица 4. Показатели TaskId, Iterations, StartTime после усложнения обработки каждой итерации цикла

Таким образом, результаты апробации метода Parallel.For показывают, что в ходе повторных запусков программы с данным методом создается различное число задач и рабочих диапазонов, отличных друг от друга. Данное поведение программы при обработке данных типа float и double приводит к неоднозначности результата выполнения делегата localFinally, определяющего финальное действие с локальным результатом каждой задачи.

Чтобы обеспечить высокую точность проводимых вычислений, следует обеспечить переход на тип decimal:

object locker = new object();

decimal grandTotal = 0;

Parallel.For(1, 10000000,

ᅠ() => (decimal)0,

ᅠ(i, state, localTotal) =>

ᅠᅠlocalTotal + (decimal)Math.Sqrt(i),

ᅠlocalTotal =>

ᅠᅠ{ lock (locker) grandTotal += localTotal; }

);

grandTotal.Dump();

Такой переход сопряжен с накладными расходами по быстродействию программы (при вычислении суммы квадратных корней чисел от 1 до 10⁷ на четырехъядерном процессоре Intel Core i5 9300H время выполнения составляет приблизительно 0,260 мсек. при использовании типа decimal, в то время как при использовании типа double это занимает лишь 0,02 мсек.) и может быть неоправданным из-за отсутствия необходимости в результатах повышенной точности. Однако взамен на выходе обеспечивается однозначный результат: 21081849486,44249240077608.

Заключение

Точность вычислений имеет большое значение в параллельном программировании, особенно при решении сложных научных задач или задач, связанных с обработкой больших объемов данных. В параллельном программировании, когда вычисления выполняются на многопроцессорных системах, точность вычислений может быть нарушена из-за нескольких причин:

• Проблемы с синхронизацией данных – когда несколько процессоров обрабатывают одни и те же данные, возможно необходимо синхронизировать вычисления между процессорами, чтобы результаты были согласованы и точны.
• Проблемы с коммуникацией – когда процессы обмениваются данными, возможны проблемы с задержками и утечками данных, которые могут привести к ошибкам в вычислениях.
• Проблемы с точностью округления – некоторые операции вычислений могут приводить к потере точности, особенно при использовании типов данных с плавающей запятой. При распределенных вычислениях на многопроцессорных системах потеря точности может быть усугублена.

В статье особое внимание уделено последней причине на примере использования метода For класса Parallel в рамках исполняющей среды .NET Framework. Проведен анализ метода Parallel.For, исследована работа параллельной программы вычисления суммы квадратных корней заданного диапазона чисел. Выявлено, что причина неоднозначности результатов вычислений является комплексной и связана с ошибками округления вещественных чисел и порциональной обработкой диапазона чисел в потоках пула. Для уменьшения этой неоднозначности целесообразно использовать более точные типы данных, также представляет интерес применения алгоритмов, которые уменьшают влияние ошибок округления и улучшают согласованность результатов между потоками ^[10].